Monoidal categories
We know that monoids are one of the most basic algebraic structures on which many others are built. Naturally, they’re one of the first concepts we want to categorify. That is, we want to consider a category with some extra structure making its objects behave like a monoid.
So let’s charge ahead and try to write down what this means. We need some gadget that takes two objects and spits out another. The natural thing to use here is a functor . We’re using the same symbol we did for tensor products — and for a good reason — but we don’t need it to be that operation.
Now we need this functor to satisfy a couple rules to make it like a monoid multiplication. It should be associative, so for all objects
,
, and
in
. There should be an “identity” object
so that
for all objects
.
We know that the natural numbers form a monoid under multiplication with
as the identity, and we know that the category
of finite sets categorifies the natural numbers with Cartesian products standing in for multiplication. So let’s look at it to verify that everything works out. We use
as our monoidal structure and see that
… but it doesn’t really. On the left we have the set
, and on the right we have the set
, and these are not the same set. What happened?
The problem is that the results are not the same, but are only isomorphic. The monoid conditions are equations
So when we categorify the concept we need to replace these by natural isomorphisms
These say that while the results of the two functors on either side of the arrow might not be the same, they are isomorphic. Even better, the isomorphism should commute with arrows in , as described by the naturality squares. For instance, if we have an arrow
in
then we can apply it before or after
:
as arrows from
to
.
As a side note, the isomorphism is often called the “associator”, but I don’t know of a similarly catchy name for the other two isomorphisms. When we’ve “weakened” the definition of a monoidal category like this we sometimes call the result a “weak monoidal category”. Alternatively — and this is the convention I prefer — we call these the monoidal categories, and the above definition with equalities instead of just isomorphisms gives “strict monoidal categories”.
Unfortunately, we’re not quite done with revising our definition yet. We’ll be taking our tensor products and identity objects and stringing them together to make new functors, and similarly we’ll be using these natural isomorphisms to relate these functors, but we need to make sure that the relationship doesn’t depend on how we build it from the basic natural isomorphisms. An example should help make this clearer.

This is the pentagon diagram. The vertices of the pentagon are the five different ways of parenthesizing a product of four different objects. The edges are single steps, each using one associator. Around the left, we apply the associator to the first three factors and leave alone (use the identity arrow
), then we apply the associator to
,
, and
, and finally we apply the associator to the last three factors and leave
alone. Around the right, we apply the associator twice, first to
,
, and
, and then to
,
, and
. So we have two different natural isomorphisms from
to
. And we have to insist that they’re the same.
Here’s another example:
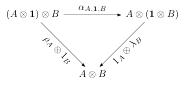
This triangle diagram is read the same as the pentagon above: we have two different natural transformations from to
, and we insist that they be the same.
What’s happened is we’ve replaced equations at the level of sets with (natural) isomorphisms at the level of the category, but these isomorphisms are now subject to new equations. We’ve seen two examples of these new equations, and it turns out that all the others follow from these two. I’ll defer the justification of this “coherence theorem” until later.
For now, let’s go back to We can use the universal property of the product to give an arrow
, and we can verify that these form the components of a natural isomorphism. Similarly, we can use the singleton
as an identity object and determine isomorphisms
and
. They do indeed satisfy the pentagon and triangle identities above, making
into a monoidal category.
In fact, you could establish the associator and other isomorphisms for by looking at the elements of the sets and defining particular functions, but if we do it all by the universal properties of products and terminal objects we get a great generalization: any category with finite products (in particular, pairwise products and a terminal object) can use them as a monoidal structure. Dually, any category with finite coproducts can use them as a monoidal structure.
For any ring , the category
of all
bimodules has a monoidal structure given by
, and because of this monoidal categories are often called “tensor categories” and the monoidal structure a tensor product.

[…] Lane’s Coherence Theorem Okay, as I promised yesterday, I’m going to prove the Coherence Theorem for monoidal categories today. That is, any two […]
Pingback by Mac Lane’s Coherence Theorem « The Unapologetic Mathematician | June 29, 2007 |
[…] Functors and Natural Transformations Now that we’ve got monoidal categories as the category-level analogue of monoids we need the category-level analogue of monoid […]
Pingback by Monoidal Functors and Natural Transformations « The Unapologetic Mathematician | June 30, 2007 |
[…] and Symmetries So we’ve got monoidal categories that categorify the notion of monoids. In building up, we had to weaken things, refusing to talk […]
Pingback by Braidings and Symmetries « The Unapologetic Mathematician | July 2, 2007 |
[…] with Duals Now we’ve got monoidal categories to categorify the notion of a monoid, we should consider what the proper analogue of an inverse is. […]
Pingback by Categories with Duals « The Unapologetic Mathematician | July 7, 2007 |
[…] last example along these lines, let’s throw all these structures in together. We start with a monoidal category, and we want it to have both a braiding and duals. Naturally, they’ll have to play well […]
Pingback by Braided Monoidal Categories with Duals « The Unapologetic Mathematician | July 13, 2007 |
[…] monoidal category has an “identity” object , so to make it a bit more interesting let’s throw in a […]
Pingback by Monoid Objects « The Unapologetic Mathematician | July 23, 2007 |
[…] Now we want to take our 2-categories of spans and add some 2-categorical analogue of a monoidal structure on […]
Pingback by Monoidal Structures on Span 2-Categories « The Unapologetic Mathematician | October 11, 2007 |
[…] The Category of Matrices II As we consider the category of matrices over the field , we find a monoidal structure. […]
Pingback by The Category of Matrices II « The Unapologetic Mathematician | June 3, 2008 |
Surely on the pentagon diagram, the bottom associator shouldn’t have that first alpha; it doesn’t seem to make sense as it stands.
Heh.. Looks like you caught a typo nobody else did. I’ll get on that.
There. Is that better? If nothing else it gave me the excuse to get the commutative diagrams package installed on my new computer.
[…] Representations of Bialgebras What’s so great about bialgebras? Their categories of representations are monoidal! […]
Pingback by Representations of Bialgebras « The Unapologetic Mathematician | November 11, 2008 |
[…] But the 2-category language gives us a bit more flexibility. Instead of demanding that the morphism satisfy the associative law on the nose, we can add a “coassociator” 2-morphism to our model 2-category. Similarly, we dispense with the left and right counit laws and add left and right counit 2-morphisms. Then we insist that these 2-morphisms satisfy pentagon and triangle identities dual to those we defined when we talked about monoidal categories. […]
Pingback by The Category of Representations of a Hopf Algebra « The Unapologetic Mathematician | November 18, 2008 |
What about right and left unitors for rho and lambda (as used by Baez and Stay). Somehow this makes me think of Skeletor, Megatron, and other figures from when my kids were small, but that should make it more fun …
You’re going to hate me for this, Avery, but I dislike “unitor” partly because it reminds me of the Transformers from when I was small.
Interesting shared association. My wife thought it was hilarious
Hmm how about left & right `unitals’ for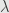 and
and 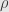 ?
?
[…] category is also monoidal closed. There are various natural monoidal structures we could use, so we’ll start with the […]
Pingback by Ordered Linear Spaces II « The Unapologetic Mathematician | May 15, 2009 |
What is the relation between universal property of tensor products (a la modules) and the tensor product in a monoidal category? Does this monoidal product satisfy some universal property?
The monoidal product in a monoidal category doesn’t need to satisfy any universal property. It just has to come with an associator and left and right unit isomorphisms.
Suppose the category is k-linear and has internal Hom. Actually I’m referring to a paper which explains this connexion but I can’t recall which. It’s not axiomatic for monoidal categories but is a result if certain things are assumed for \mathcal{C}.
Giusto, for more on universal properties and monoidal categories, you might want to look at the interconnections between multicategories and monoidal categories as described in Tom Leinster’s book, Higher Operads, Higher Categories. Specifically, see pages 82-87 (pages 112-117 of the pdf file here, where an equivalence between monoidal categories and representable multicategories is given. This gives the sought-after interpretation which generalizes the sense in which tensor products of bimodules are universal with respect to multilinear maps.
[…] in the above exercise behaves like an associator, like we talked about in the context of monoidal categories. And, just like in that case, we will find left and right identity […]
Pingback by Homotopies as Morphisms « The Unapologetic Mathematician | November 29, 2011 |