The Fundamental Theorem of Calculus I
Today we get to the Fundamental Theorem of Calculus, which comes in two parts. This theorem is essential, in that it shows how the two seemingly-dissimilar fields of integral and differential calculus are actually two sides of the same coin. From this point, most of the basic theory of integration comes down to finding the “mirror image” of facts about differentiation.
First, let’s start with some continuous function and define a new function by
. Now the fundamental theorem tells us that this new function is differentiable, and its derivative is the function we started with! That is:
To see this, let’s consider the difference . The first term here is the integral
. Then we can split this interval up to get the sum of the integrals
. But the first part here is just
, which we’re about to subtract off. Then the difference quotient is
. The derivative
will be the limit of this difference quotient as
goes to
.
So now let’s use the Integral Mean Value Theorem to get at the integral here. It tells us that there’s some between
and
with
— the difference quotient exactly! And as
gets smaller and smaller,
gets squeezed closer and closer to
. And because
is continuous, we find that
. Presto!
A very common metaphor here is to think of a carpet whose width at a point along its length is
. Then its total area from the starting point
up to
is the integral
. How fast is the area increasing as we unroll more carpet? As we unroll
more length we get
more area, and so the derivative of the area is the width of the carpet.

Oh-oh-oh! The same pathetic proof that mixes apples and oranges, and makes the reader believe that MVT has anything to do woth FTC! Please, spare me!
And yet I still see no offering from you. Somehow we must soldier on, bereft of your sagacity. Maybe you’ll consider tomorrow’s proof to be worthy of your time.
By the way, a few days ago I stumbled across a really nice introductory calculus book by Zeldovich and I.M. Yaglom, called “Higher Math for Beginners.” It’s out of print, but you can download id via P2P or from my web page
It still has limits, but goes easy on them. Take a look.
Actually I’m seriously thinking about getting my own blog to present calculus as it should be presented, simply and clearly. Do you think it’s worth the effort?
If it provides you some outlet other than kibbutzing about how horribly I’m doing everything over here (because obviously I can’t just have a different point of view than you — I must be wrong), then go for it. Go spread your gospel elsewhere instead of just bitching and moaning about me.
Damn, I messed up the link! Let me try again: book
Don’t you think that my bitching and moaning somewhat enlivens your blog?
I also want to save your soul, you went astray,I want to bring you back to papa Newton!
No, not really. I don’t mind having a community of lurkers (and it’s evidently somewhat sizable, judging my the traffic logs).
You’re a gadfly, and nothing but. You don’t really have anything to add of your own, but only criticism for someone who actually steps up and takes a swing.
I know that there are other ways of approaching the exact same subject, but for you there is only the One True Faith, and that position is anathema to actual mathematics. I’m not saying your approach is wrong, but you come back time and again and say that I’m not just different, but actually incorrect. There are more things in Heaven and Earth than are dreamt of in your analysis, Michael. Maybe that explains why you washed out.
Here is an interesting article by V.I. Arnold about math education. Enjoy.
…but for you there is only the One True Faith… Really? Do I come across like this, or you just want to piss me off? Acually I never said you were wrong in what you wrote, formally speking, what you write is correct, I just questioned whether your approach is reasonable. And speaking about contributing anything new, what you write about elementary analysis is written many times over in every book on the subject you can pick at any library. Sorry, I didn’t mean to get nasty.
Michael, you seem to yet again confuse my exposition here for a calculus lecture. You seem to be under the impression that this is how I actually teach the material in a classroom.
I suppose it’s clear that since you can only see one way to present the subject, the same must be true of me, right? I must be going off about compacta and subnets to poor first-semester calculus students, and throwing out both the geometric intuition and the emphasis on being able to solve problems.
Michael, I’ve told you time and again: I know many ways to present the subject. I’m making a choice here to present it this way. It has its benefits and its flaws, but you’re so narrow-minded and short-sighted that all you can do is complain that it’s not your own precious way.
I didn’t prove the integral MVT from the FToC right away because I wanted to use it in this proof here. Then there’s another proof for part 2, with a distinct flavor. Then there’s the connections between the two parts. Then there’s using the FToC as a mirror to reflect differential to integral calculus and vice versa. And there are plenty of threads I’m not following. And still all you can do is throw a tantrum over how it’s not your way.
So put up or shut up, Michael. Get your own weblog and present the material your way, in your style, at your pace. Make your own choices and speak your own mind. I certainly won’t begrudge the competition, because I don’t think there is a competition. You like certain aspects of the theory and I like others, and that’s all there is to it.
But I still don’t think you’ll do it. You don’t have anything to create of your own. You just know how to tear at others’ work rather than to build anything yourself. If you did start a weblog, it would only be a soapbox to trumpet your One True Faith, and that small, selfish motive can only act as a mirror, trying vainly to reflect glory back on yourself.
Go, Michael. Create something for once, and maybe you’ll find it more redeeming than the sickly, wretched life of a troll, existing only to pick fights.
“One True Faith?” Isn’t it how your Church of Limitology operates, shoe-horning everything that movers into limits?
I have already created an approach to calculus that many people find more reasonable than your dry as dust ideology of limits. Only time will tell which one is better.
Yeah, you talk a lot about having created it. I still see little evidence. You cite one essay after another by luminaries, and criticize my approach as “dry”.
But what’s so “dry” about it? The limiting process of a net is a marvelously rich process. If I were trying to teach someone how to use the basic tools (like in a calculus course), it’s probably a little high-tech. But if I were, say, writing a weblog trying to tie in the basics of calculus to topology, and to leave threads connecting all the way back to category theory, it’s just what the doctor ordered.
Again, you’re the one attacking me for failing to do something I’m not even trying to do. You can’t see calculus exposition as anything but an introductory lecture course, which I keep trying to say is not what I’m doing here.
You hang around here, always ready with your shrill “NO, NO, NO”, rather than ever moderate with a “yes, but”. You show no evidence of even trying to understand why I might make different choices than you do. You’re just a complainer. Just a troll.
I still don’t see you creating. Still just picking away.
O.K. Yes, but the proof of FTC presented in this posting sucks. Let’s see what the next proof will look like.
Yes, it’s fine to show how elementary analysis can be seen as an application of convergence of the nets, but to claim that the only way to do calculus “rigorously” is by limits and brush off any other approach as “mnemonics” is an example of narrow-mindedness that you claim to oppose.
The only thing I said was a mnemonic is when you asserted that the derivative is a quotient. Which it simply isn’t. It shares a lot of notational similarities with quotients, but you’re constantly sloppy about the ring it’s supposed to live in, and the whole thing breaks down once you try to move on to functions of more than one variable.
And I actually do tell my students that it behaves something like a quotient, and I even introduce the gradient in calculus 3 from the desire to have a quotient, but the best we can do is find “what we have to multiply the change in input by to estimate the change in output”. There’s a lot of similarities to quotients, but there’s a difference between “like” and “is”, and that’s a line I draw brightly precisely because it does break down just a couple semesters later.
You see, I have my reasons for taking the approaches here I do, and for taking the approaches in class that I do, and the two approaches I take aren’t always the same. But you complain that on this weblog I’m not using the approach you think is best for teaching a class (hint: a weblog is not a class). And even if we were comparing classroom presentations, I have seen the approach you so stridently insist upon (long before I’d ever heard of you, mind you) and have decided on another course.
I really can’t see why you take it so personally that I disagree with you. I get good results with my pedagogy, and you get good results with yours. Why is it so offensive to you that I don’t make the same choices that you do in class? Why is it so offensive to you that I don’t make the same choices on this weblog (which, again, is not a class) as you would make in a class?
I think you should. It would be a lot more constructive than what you’re doing here, and it may well give you pleasure.
I think John said somewhere that he gets several hundred hits per day (300-500, or something), which means about that many people will have already seen your name and roughly where you’re coming from. In other words, you may well have a ready-made audience.
I’m not clear how thoroughly you’ve worked out your ideas; this would be an interesting crucible. I think you can expect that a lot of people — including some very smart people — would be examining your efforts very closely, and yes, offering criticism. Some of it may be very negative and personal as well, as John could tell you. Are you up to it? Could you take the heat?
There’s a saying: put up or shut up. So, what do you say?
John, for what it’s worth, I read your blog every day. I’ve been away from math for many years and have a lot of reviewing and catching up to do before I can ever hope to understand what’s going on in the world today. For me, your lessons achieve the perfect balance between rigor and pragmatism. They are helping me to advance far faster than I had ever hoped. And they are fun too! You have taken on a very difficult task, and as far as I’m concerned, your contributions are extremely useful and your teaching method successful. I can’t imagine a more efficient and enjoyable way for me to gain a solid foundation to which to build. Thank you!
Charlie, thanks. I know there are a fair number of people out there reading. I’m not as big as, say, Scott Aaronson is (or maybe I just don’t post on controversial subjects as much), but there’s an audience. And so I don’t really mind if one cranky reader decides he’s going to make it his personal mission to whine about how I do everything.
And while we’re at the “statements of support” – obviously, you would have noticed that I read pretty much all your posts.
And I started this precisely because the expositional style and level your blog had when I stumbled across it (and keeps up for at least some of the subjects you cover) is extremely interesting and well-written.
Yes, but let me esplain why I don’t like the proof of FTC in this posting. You see, this theorem has a simple generalization that does not assume that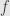 is continouous on the whole interval
is continouous on the whole interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=e6e6e6&fg=333333&s=0&c=20201002) , it only requires
, it only requires 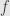 to be Riemann-integrable and coninuous at the point
to be Riemann-integrable and coninuous at the point  , and it says that
, and it says that
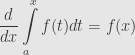
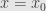
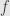 can be discontinuous on a set of measure zero, and John’s prove does not apply. But a proof that uses positivity of the Riemann integral i.e., the fact that positive functions have positive integrals still works.
can be discontinuous on a set of measure zero, and John’s prove does not apply. But a proof that uses positivity of the Riemann integral i.e., the fact that positive functions have positive integrals still works.
for
Now,
When I saw that this post had 20 comments, I wondered what could possibly be so controversial about the fundamental theorem of calculus. My word!
I am one of the clueless undergraduates this fellow seems so bent on saving from your teaching methods, and I find this blog to be an extremely valuable resource.
Yes, you are, Patricia. If you think that the mean value theorem has anything to do with the fundamental theorem of calculus, you are a misguided soul and better cleanse your brain from all the prejudices you got indoctrinated with in your calculus class, or you will go directrly to hell! 😀
Ahh, Michael. Now you get a little closer to actually stating a positive (sorry) point.
First: I never claimed that the proof was the most expansive one possible.
Second: You’re still not giving an actual proof. You’re scrabbling at the roots of one, but you’re oh-so-cleverly impish and can’t bear actually coming out and saying anything. No matter. You’ve given enough away that I know..
Third: Behind all of this moaning, you’re actually thinking about the proof I was going to come back to once I get to measure theory, and do the whole thing over with the Lebesgue integral. Notice that you’re talking already in terms of “measure zero”, and I haven’t even mentioned measure once. Maybe that has something to do with why I’m not giving that extended context to the theorem?
I’m not answering this matter any more. I leave you with Dante:
Michael Livshits:
You remind me of my number theory professor. Sometimes I think the only reason he doesn’t bite me is because, as he’s said, “human flesh is not kosher.”
Now, here is the proof (of the theorem I formulated in response #20) that I had in mind, just in case anybody hasn’t figured it out yet. We have to prove that , which is the same as
, which is the same as 
 , there we can find positive
, there we can find positive 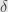 such that
such that  when
when 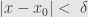 . For such
. For such  the absolute value of the last integral will be less than
the absolute value of the last integral will be less than  and we are done.
and we are done.
Now, given positive
To John: I wish this web page had a preview feature, or replace feature or something like that… I’m thinking why that damn latex did not parse! To Patricia: what’s wrong? I just pointed some triviality to you.
The integral that I was talking about was $latex \displaystyle\int\limits_{x_0}^xf(t)-f(x_0)dt
The integral that I was talking about was
John, what made me all wound up about you prrof is that you drag in some rather subtle result (the MVT) that is not needed at all to prove your theorem. It’is a really bad taste to do such things, and it makes rour proof misleading rather that clarifying the matter. But it looks like a proof is a proof is a proof to you, no matter how ugly.
[…] Theorem of Calculus (all together now) So we’ve seen two sides of the FToC: the first part, which says that given a continuous function we can integrate and differentiate to get our […]
Pingback by The Fundamental Theorem of Calculus (all together now) « The Unapologetic Mathematician | February 15, 2008 |
[…] Flame War Wrap-Up Well, we’ve certainly had a lively time the last few days. Regular commentercomplainer Michael Livshits kicked it off by noting that I presented The […]
Pingback by FToC Flame War Wrap-Up « The Unapologetic Mathematician | February 16, 2008 |
Michael the yellow&red thing is a real bore.
so preview it in your own damn site;
then cut-and-paste the (tested) code.
[…] We proved some properties about the functions we get like this, lining them up against the Fundamental Theorem of Calculus. In particular, integrating like this can construct […]
Pingback by The Natural Logarithm « The Unapologetic Mathematician | April 16, 2008 |
[…] behaves a lot like the Fundamental Theorem of Calculus, in that constructing the sequence of partial sums and constructing the sequence of differences […]
Pingback by Abel’s Partial Summation Formula « The Unapologetic Mathematician | April 30, 2008 |
Shut the hell up michael. Bravo for your contribution to mankind, I’m sure you’ll make a splendid teacher, husband, and father as well.
Thanks for the support melody. Unfortunately, the job situation being what it is it’s doubtful I’ll be a teacher for much longer. And the world situation being what it is, husband seems unlikely, let alone father.
[…] results are similar to those we get from the Fundamental Theorem of Calculus, and we can use some of the same techniques to prove them. In particular, we call on the Integral […]
Pingback by The Integral as a Function of the Interval « The Unapologetic Mathematician | March 14, 2009 |
[…] A neat little variation on differentiating an integral from last time combines it with the fundamental theorem of calculus. It’s especially interesting in the context of evaluating iterated integrals for irregular […]
Pingback by Differentiating Partial Integrals « The Unapologetic Mathematician | January 14, 2010 |