Polar Decomposition

Okay, let’s take the singular value decomposition and do something really neat with it. Specifically, we’ll start with an endomorphism $T:A\rightarrow A$ and we’ll write down its singular value decomposition

$\displaystyle T=V\Sigma W^*$

where $V$ and $W$ are in the unitary (orthogonal) group of $A$ . So, as it turns out, $U=VW^*$ is also unitary. And $P=W\Sigma W^*$ is positive-semidefinite (since $\Sigma$ is). And, of course, since $W^*W=1_A$ , we can write

$\displaystyle T=V\Sigma W^*=VW^*W\Sigma W^*=UP$

That is, any endomorphism can be written as the product of a unitary transformation and a positive-semidefinite one.

Remember that unitary transformations are like unit complex numbers, while positive-semidefinite transformations are like nonnegative real numbers. And so this “polar decomposition” is like the polar form of a complex number, where we write a complex number as the product of a unit complex number and a nonnegative real number.

We can recover the analogy like we did before, by taking determinants. We find

$\displaystyle\det(T)=\det(U)\det(P)=e^{i\theta}r$

since the determinant of a unitary transformation is a unit complex number, and the determinant of a positive-semidefinite transformation is a nonnegative real number. If $T$ is nonsingular, so $P$ is actually positive-definite, then $\det(P)$ will be strictly positive, so the determinant of $T$ will be nonzero.

We could also define $P'=W\Sigma W^*$ , so $T=P'U$ . This is the left polar decomposition (writing the positive-definite part on the left), where the previous form is the right polar decomposition

August 19, 2009 - Posted by John Armstrong | Algebra, Linear Algebra

7 Comments »

What if I don’t want to ” take the singular value decomposition”? Your entire argument collapses.

NS

Comment by notedscholar | August 19, 2009 | Reply
That’s the nice thing about mathematics. My argument doesn’t collapse just because you hold your breath and stamp your feet.

Comment by John Armstrong | August 19, 2009 | Reply
Is the decomposition T=UP unique in any sense?

Comment by Å | August 20, 2009 | Reply
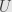The positive-definite part $P$ is unique (I’ll be able to say more about that after today’s post), and from that point $U$ is also unique exactly when 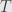$T$ (and thus $P$ ) is nonsingular.

Comment by John Armstrong | August 20, 2009 | Reply
[…] Uniqueness of Polar Decomposition I asserted in a comment that the polar decomposition of a transformation has certain uniqueness properties. First, we can always uniquely recover the […]

Pingback by The Uniqueness of Polar Decomposition « The Unapologetic Mathematician | August 21, 2009 | Reply
Right. But it does collapse if we don’t grant your premises.

NS

Comment by notedscholar | August 21, 2009 | Reply
[…] used this to show in particular if is an endomorphism on an inner product space we can write where is unitary and […]

Pingback by Decompositions Past and Future « The Unapologetic Mathematician | August 24, 2009 | Reply

About this weblog

This is mainly an expository blath, with occasional high-level excursions, humorous observations, rants, and musings. The main-line exposition should be accessible to the “Generally Interested Lay Audience”, as long as you trace the links back towards the basics. Check the sidebar for specific topics (under “Categories”).

I’m in the process of tweaking some aspects of the site to make it easier to refer back to older topics, so try to make the best of it for now.

RSS Feeds

RSS - Posts
RSS - Comments
Feedback

Got something to say? Anonymous questions, comments, and suggestions at Formspring.me!
Subjects

Subjects
Archives

August 2009

M T W T F S S

1 2

3 4 5 6 7 8 9

10 11 12 13 14 15 16

17 18 19 20 21 22 23

24 25 26 27 28 29 30

31

« Jul Sep »
Search for:

The Unapologetic Mathematician

Mathematics for the interested outsider