The Radon-Nikodym Theorem (Proof)

Today we set about the proof of the Radon-Nikodym theorem. We assumed that $(X,\mathcal{S},\mu)$ is a $\sigma$ -finite measure space, and that $\nu$ is a $\sigma$ -finite signed measure. Thus we can write $X$ as the countable union of subsets on which both $\mu$ and $\nu$ are finite, and so without loss of generality we may as well assume that they’re finite to begin with.

Now, if we assume for the moment that we’re correct and an $f$ does exist so that $\nu$ is its indefinite integral, then the fact that $\nu$ is finite means that $f$ is integrable, and then if $g$ is any other such function we can calculate

$\displaystyle\int\limits_Ef-g\,d\mu=\int\limits_Ef\,d\mu-\int\limits_Ef\,d\mu=\nu(E)-\nu(E)=0$

for every measurable $E\in\mathcal{S}$ . Now we know that this implies $f-g=0$ a.e., and thus the uniqueness condition we asserted will hold.

Back to the general case, we know that the absolute continuity $\nu\ll\mu$ is equivalent to the conjunction of $\nu^+\ll\mu$ and $\nu^-\ll\mu$ , and so we can reduce to the case where $\nu$ is a finite measure, not just a finite signed measure.

Now we define the collection $\mathcal{K}$ of all nonnegative functions $f$ which are integrable with respect to $\mu$ , and for which we have

$\displaystyle\int\limits_Ef\,d\mu\leq\nu(E)$

for every measurable $E$ . We define

$\displaystyle\alpha=\sup\limits_{f\in\mathcal{K}}\int f\,d\mu$

Since $\alpha$ is the supremum, we can find a sequence $\{f_n\}$ of functions in $\mathcal{K}$ so that

$\displaystyle\lim\limits_{n\to\infty}\int f\,d\mu=\alpha$

For each $n$ we define

$\displaystyle g_n(x)=\max\limits_{1\leq i\leq n}f_i(x)$

Now if $E$ is some measurable set we can break it into the finite disjoint union of $n$ sets $E_i$ so that $g_n=f_i$ on $E_i$ . Thus we have

$\displaystyle\int\limits_Eg_n\,d\mu=\sum\limits_{i=1}^n\int\limits_{E_i}f_i\,d\mu\leq\sum\limits_{i=1}^n\nu(E_i)=\nu(E)$

and so $g_n\in\mathcal{K}$ .

We can write $g_n=g_{n-1}\cup f_n$ , which tells us that the sequence $\{g_n\}$ is increasing. We define $f_0$ to be the limit of the $g_n$ — $f_0(x)$ is the maximum of all the $f_i(x)$ — and use the monotone convergence theorem to tell us that

$\displaystyle\int_Ef_0\,d\mu=\lim\limits_{n\to\infty}\int_Eg_n\,d\mu$

Since all of the integrals on the right are bounded above by $\nu(E)$ , their limit is as well, and $f_0\in\mathcal{K}$ . Further, we can tell that the integral of $f_0$ over all of $X$ must be $\alpha$ . Since $f_0$ is integrable, it must be equal $\mu$ -a.e. to some finite-valued function $f$ . What we must now show is that if we define

$\displaystyle\nu_0(E)=\nu(E)-\int\limits_Ef\,d\mu$

then $\nu_0$ is identically zero.

If it’s not identically zero, then by the lemma from yesterday there is a positive number $\epsilon$ and a set $A$ so that $\mu(A)>0$ and so that

$\displaystyle\epsilon\mu(E\cap A)\leq\nu_0(E\cap A)=\nu(E\cap A)-\int\limits_{E\cap A}f\,d\mu$

for every measurable set $E$ . If we define $g=f+\epsilon\chi_A$ , then

$\displaystyle\int\limits_Eg\,d\mu=\int\limits_Ef\,d\mu+\epsilon\mu(E\cap A)\leq\int\limits_{E\setminus A}+\nu(E\cap A)\leq\nu(E)$

for every measurable set $E$ , which means that $g\in\mathcal{K}$ . But

$\displaystyle\int g\,d\mu=\int f\,d\mu+\epsilon\mu(A)>\alpha$

which contradicts the maximality of the integral of $f$ . Thus $\nu_0$ must be identically zero, and the proof is complete.

July 7, 2010 - Posted by John Armstrong | Analysis, Measure Theory

3 Comments »

nice

Comment by samah | March 16, 2011 | Reply
Hi, thanks for this great blog, but I have a question which is probabaly quite obvious but I am not sure how you can say that there exiist a sequence which converges to alpha, please could you explain. Thanks a lot

Comment by Marco | September 6, 2011 | Reply
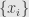It’s actually a basic analytic statement: if $x$ is the supremum of a collection of real numbers $\{x_i\}$ , then there is some sequence of the $x_i$ converging to $x$ . If there weren’t, then there’s some neighborhood of $x$ that the $x_i$ never get into, and so any number below $x$ in that neighborhood would be a lower upper bound of the set.

Comment by John Armstrong | September 6, 2011 | Reply

About this weblog

This is mainly an expository blath, with occasional high-level excursions, humorous observations, rants, and musings. The main-line exposition should be accessible to the “Generally Interested Lay Audience”, as long as you trace the links back towards the basics. Check the sidebar for specific topics (under “Categories”).

I’m in the process of tweaking some aspects of the site to make it easier to refer back to older topics, so try to make the best of it for now.

RSS Feeds

RSS - Posts
RSS - Comments
Feedback

Got something to say? Anonymous questions, comments, and suggestions at Formspring.me!
Subjects

Subjects
Archives

July 2010

M T W T F S S

1 2 3 4

5 6 7 8 9 10 11

12 13 14 15 16 17 18

19 20 21 22 23 24 25

26 27 28 29 30 31

« Jun Aug »
Search for:

The Unapologetic Mathematician

Mathematics for the interested outsider