Amalgamated free products
I was thinking that one thing might have been unclear in my discussion of free products. The two groups in the product must be completely disjoint — there are no elements in common. Particularly, if we take the free product 
we must use two different — but isomorphic — copies of 
. For example, in 
we might take the first copy of 
to be permutations of 
, and the second to be permutations of 
.
So what if the groups aren’t disjoint? Say they share a subgroup. There’s a tool we can use to handle this and a few other situations: the amalgamated free product. Here’s the picture:
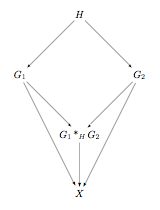
This diagram looks a lot like the one for free products, but it has the group 
up at the top and homomorphisms from into each of 
and 
, and we insist that the square commutes. That is, we send an element of into and on into 
or we can send it into and on into , and the result will be the same either way. In many cases will be a common subgroup of and , and the homomorphisms from are just the inclusions.
So how do we read this diagram? We start with three groups and two homomorphisms — 
— and we look for groups that “complete the square”. The amalgamated free product is the “universal” such group — given any other group 
that completes the square there is a unique homomorphism from to .
Just like for free products we’ve given a property, but we haven’t shown that such a thing actually exists. First of all there should be a homomorphism from 
to by the universal property of . Then we have two ways of sending into : send to sitting inside or send it to inside . Let’s call the first way 
and the second way 
. Now we want to add the relation 
for each element of . That is, 
should be the identity. It isn’t the identity in , but we can make it the identity by taking the smallest normal subgroup 
of containing all these elements and moving to the quotient 
. This is the group we’re looking for.
We’ve shown that does complete the square. Now if is any other group that completes the square it has homomorphisms into it from each of and , so there’s a unique homomorphism 
. But now 
sends every element of to the identity in because we assumed that makes the outer square in the diagram commute. Since is in the kernel of we get a well-defined homomorphism from to , which is the one we need.
Amalgamated free products will become very important somewhere down the road, especially because they (and related concepts) figure very prominently in my own work.
March 3, 2007 -
Posted by John Armstrong |
Algebra, Group theory, Structure of Groups, Universal Properties
The Unapologetic Mathematician 
[…] modules, more ideals The first construction I want to run through today is related to the amalgamated free product from group theory. Here’s the diagram in modules: Remember we read it as follows: If we have […]
Pingback by More modules, more ideals « The Unapologetic Mathematician | May 10, 2007 |
Hi, as a newbie to algebraic topology, I found your blog to be really helpful. I’m therefore trying to be unapologetic of asking obvious (to others) questions:
When you say (G1*G2)/N completes the square, do you put (G1*G2)/N in place of G1*G2 or in place of X in the diagram?
Also, I’m confused about your statement: The two groups in the product must be completely disjoint . Although you assumed G1 and G2 to be non-disjoint, the derivation of (G1*G2)/N still involves the universal property of G1*G2.
Sorry for the delay, Tori.
In answer to your first question, imagine erasing everything below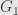
and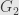 
so the square is incomplete. There may be many different ways of “completing the square” here — 
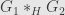and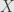 
both complete the square, for example — but we’re looking for a “universal” one, which has a unique arrow into any other such completion that makes both triangles commute.
As for the derivation of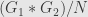
, I may have glossed over the idea that when we construct this free product we pretend that the groups are completely disjoint. One way around it is to make an isomorphic copy of 
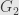which is disjoint from 
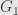; it doesn’t matter if the arrows from 
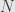into 
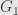and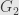 
are “really” inclusions or just mappings.
hth
Thanks for the explanation!
One question about these push-outs. It is known that if both the morphisms $H\to G_i$ in your diagram are injective, then their corresponding mirror images morphisms $G_i\to G_1\star_H G_2$ are also injective. Is is true, as it happends in other categories, than just having one of them injective, say $H\to G_1$, then its mirror morphism $G_2\to G_1\star_H G_2$ is injective as well? Thanks for your time.
I’m sorry to say I don’t know offhand. I’d suggest you take the proof of that fact that you know in one category and try to replicate it without referring to the specifics of that category.
[…] The Unapologetic Mathematician. […]
Hello, first of all, very nice explanation of amalgamated product, it helped me to undersand it!
When you are adding the relation f_1(h)=f_2(h), why are the functions f_1 and f_2 going from H to G_1*G_2, and not from H to respectively G_1 and G_2 (as I have seen in some definitions of amalgamated product)?
One might also write $f_i: H\to G_i$. Then one considers the canonical inclusions $\iota_i: G_i\to G_1*G_2$. Composing these, one gets the maps $f_i\circ\iota_i: H\to G_1*G_2$, one of which factors through $G_1$ and the other through $G_2$.
I was just skipping over the middle to write $f_i$ as the appropriate composition right away.