Uses of the Jordan-Chevalley Decomposition

Now that we’ve given the proof, we want to mention a few uses of the Jordan-Chevalley decomposition.

First, we let $A$ be any finite-dimensional $\mathbb{F}$ -algebra — associative, Lie, whatever — and remember that $\mathrm{End}_\mathbb{F}(A)$ contains the Lie algebra of derivations $\mathrm{Der}(A)$ . I say that if $\delta\in\mathrm{Der}(A)$ then so are its semisimple part $\sigma$ and its nilpotent part $\nu$ ; it’s enough to show that $\sigma$ is.

Just like we decomposed $V$ in the proof of the Jordan-Chevalley decomposition, we can break $A$ down into the eigenspaces of $\delta$ — or, equivalently, of $\sigma$ . But this time we will index them by the eigenvalue: $A_a$ consists of those $x\in A$ such that $\left[\delta-aI\right]^k(x)=0$ for sufficiently large $k$ .

Now we have the identity:

$\displaystyle\left[\delta-(a+b)I\right]^n(xy)=\sum\limits_{i=0}^n\binom{n}{i}\left[\delta-aI\right]^{n-i}(x)\left[\delta-bI\right]^i(y)$

which is easily verified. If a sufficiently large power of $\delta-aI$ applied to $x$ and a sufficiently large power of $\delta-bI$ applied to $y$ are both zero, then for sufficiently large $n$ one or the other factor in each term will be zero, and so the entire sum is zero. Thus we verify that $A_aA_b\subseteq A_{a+b}$ .

If we take $x\in A_a$ and $y\in A_b$ then $xy\in A_{a+b}$ , and thus $\sigma(xy)=(a+b)xy$ . On the other hand,

$\displaystyle\begin{aligned}\sigma(x)y+x\sigma(y)&=axy+bxy\\&=(a+b)xy\end{aligned}$

And thus $\sigma$ satisfies the derivation property

$\displaystyle\sigma(xy)=\sigma(x)y+x\sigma(y)$

so $\sigma$ and $\nu$ are both in $\mathrm{Der}(A)$ .

For the other side we note that, just as the adjoint of a nilpotent endomorphism is nilpotent, the adjoint of a semisimple endomorphism is semisimple. Indeed, if $\{v_i\}_{i=0}^n$ is a basis of $V$ such that the matrix of $x$ is diagonal with eigenvalues $\{a_i\}$ , then we let $e_{ij}$ be the standard basis element of $\mathfrak{gl}(n,\mathbb{F})$ , which is isomorphic to $\mathfrak{gl}(V)$ using the basis $\{v_i\}$ . It’s a straightforward calculation to verify that

$\displaystyle\left[\mathrm{ad}(x)\right](e_{ij})=(a_i-a_j)e_{ij}$

and thus $\mathrm{ad}(x)$ is diagonal with respect to this basis.

So now if $x=x_s+x_n$ is the Jordan-Chevalley decomposition of $x$ , then $\mathrm{ad}(x_s)$ is semisimple and $\mathrm{ad}(x_n)$ is nilpotent. They commute, since

$\displaystyle\begin{aligned}\left[\mathrm{ad}(x_s),\mathrm{ad}(x_n)\right]&=\mathrm{ad}\left([x_s,x_n]\right)\\&=\mathrm{ad}(0)=0\end{aligned}$

Since $\mathrm{ad}(x)=\mathrm{ad}(x_s)+\mathrm{ad}(x_n)$ is the decomposition of $\mathrm{ad}(x)$ into a semisimple and a nilpotent part which commute with each other, it is the Jordan-Chevalley decomposition of $\mathrm{ad}(x)$ .

August 30, 2012 - Posted by John Armstrong | Algebra, Lie Algebras, Linear Algebra

3 Comments »

Could you elaborate a bit (or just give me a hint) on the first “identity: … which is easily verified”? I’m not seeing it…

Thanks.

Comment by Joe English | August 30, 2012 | Reply
Run an induction on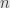 $n$ ; it works out sort of like the binomial theorem does.

Comment by John Armstrong | August 30, 2012 | Reply
[…] we know that is the semisimple part of , so the Jordan-Chevalley decomposition lets us write it as a polynomial […]

Pingback by A Trace Criterion for Nilpotence « The Unapologetic Mathematician | August 31, 2012 | Reply

About this weblog

This is mainly an expository blath, with occasional high-level excursions, humorous observations, rants, and musings. The main-line exposition should be accessible to the “Generally Interested Lay Audience”, as long as you trace the links back towards the basics. Check the sidebar for specific topics (under “Categories”).

I’m in the process of tweaking some aspects of the site to make it easier to refer back to older topics, so try to make the best of it for now.

RSS Feeds

RSS - Posts
RSS - Comments
Feedback

Got something to say? Anonymous questions, comments, and suggestions at Formspring.me!
Subjects

Subjects
Archives

August 2012

M T W T F S S

1 2 3 4 5

6 7 8 9 10 11 12

13 14 15 16 17 18 19

20 21 22 23 24 25 26

27 28 29 30 31

« Jul Sep »
Search for:

The Unapologetic Mathematician

Mathematics for the interested outsider