The Radon-Nikodym Theorem (Proof)
Today we set about the proof of the Radon-Nikodym theorem. We assumed that is a
-finite measure space, and that
is a
-finite signed measure. Thus we can write
as the countable union of subsets on which both
and
are finite, and so without loss of generality we may as well assume that they’re finite to begin with.
Now, if we assume for the moment that we’re correct and an does exist so that
is its indefinite integral, then the fact that
is finite means that
is integrable, and then if
is any other such function we can calculate
for every measurable . Now we know that this implies
a.e., and thus the uniqueness condition we asserted will hold.
Back to the general case, we know that the absolute continuity is equivalent to the conjunction of
and
, and so we can reduce to the case where
is a finite measure, not just a finite signed measure.
Now we define the collection of all nonnegative functions
which are integrable with respect to
, and for which we have
for every measurable . We define
Since is the supremum, we can find a sequence
of functions in
so that
For each we define
Now if is some measurable set we can break it into the finite disjoint union of
sets
so that
on
. Thus we have
and so .
We can write , which tells us that the sequence
is increasing. We define
to be the limit of the
—
is the maximum of all the
— and use the monotone convergence theorem to tell us that
Since all of the integrals on the right are bounded above by , their limit is as well, and
. Further, we can tell that the integral of
over all of
must be
. Since
is integrable, it must be equal
-a.e. to some finite-valued function
. What we must now show is that if we define
then is identically zero.
If it’s not identically zero, then by the lemma from yesterday there is a positive number and a set
so that
and so that
for every measurable set . If we define
, then
for every measurable set , which means that
. But
which contradicts the maximality of the integral of . Thus
must be identically zero, and the proof is complete.

nice
Hi, thanks for this great blog, but I have a question which is probabaly quite obvious but I am not sure how you can say that there exiist a sequence which converges to alpha, please could you explain. Thanks a lot
It’s actually a basic analytic statement: if is the supremum of a collection of real numbers
is the supremum of a collection of real numbers 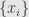 , then there is some sequence of the
, then there is some sequence of the  converging to
converging to  . If there weren’t, then there’s some neighborhood of
. If there weren’t, then there’s some neighborhood of  that the
that the  never get into, and so any number below
never get into, and so any number below  in that neighborhood would be a lower upper bound of the set.
in that neighborhood would be a lower upper bound of the set.