Dedekind Completion
There’s another sense in which the rational numbers are lacking and the real numbers fix them up. This one is completely about the order structure on 
, and will lead to another construction of the real numbers.
Okay, so what’s wrong with the rational numbers now? In any partial order we can consider least upper or greatest lower bounds. That is, given a nonempty set of rational numbers 
the least upper bound or “supremum” 
is a rational number so that 
for all 
— it’s an upper bound — and if 
is any upper bound then 
. Similarly the “infimum” 
is the greatest lower bound — a lower bound that’s greater than all the other lower bounds.
There’s just one problem: there might not be a supremum of a given set. Even if the set is bounded above, there may be no least upper bound. For instance, the set of all rational numbers 
so that 
is bounded above, since 
is an example of an upper bound, and 
is another. But no matter what upper bound we have in hand, we can always find a lower number which is still an upper bound for this set. In fact, the upper bound should be 
, but this isn’t a rational number!
Now we define an ordered field to be “Dedekind complete” if every nonempty set with an upper bound has a least upper bound . Considering the set consisting of the negatives of elements of , every nonempty set with a lower bound will have a least lower bound. The flaw in the rational numbers is that they are not Dedekind complete.
So, in order to complete them, we will use the method of “Dedekind cuts”. Given a nonempty set with any upper bounds at all, the collection of all the upper bounds forms another set 
, and any element of gives a lower bound for . We then have the collection of all lower bounds of , which we call 
. Every rational number will be in either or . Given a rational number if there is an with 
then is a lower bound for , and is thus in . If not, then is an upper bound for and is thus in . However, one number may be in both and . If has a rational supremum then it is in both and . There can be no more overlap.
So we’ve come up with a way of cutting the rational numbers into a pair of sets 
— the “left set” and “right set” of the “cut” 
— with 
for every 
and 
. We define a new total order on the set of cuts by 
if 
. Every rational number corresponds to one of the cuts which contains a one-point overlap at that rational number, and clearly this inclusion preserves the order on the rational numbers.
Now if I take any nonempty collection of cuts 
with an upper bound (in the order on the set of cuts) we can take the union of all the 
and the intersection of all the 
to get a new cut. The left set contains all the , and it’s contained in any other left set which contains them, so it’s the least upper bound. Thus the collection of cuts is now Dedekind complete.
We can also add field structures to this completion of an ordered field. For this purpose, it will be useful to denote a generic element of 
by 
, and assume runs over all elements of wherever it appears. For instance, given cuts and 
, we define their sum to be 
. The negative of a cut will be 
. The product of two positive cuts and will have as its right set the collection of all products 
, and its left set defined to make this a cut. Finally, the reciprocal of a positive cut will have the set 
as its right set, and its left set defined to make this a cut.
This suffices to define all the field operations on the set of cuts, and if we start with we get another model of 
. I’ll leave verification of the field axioms as an exercise, and come back to prove that the method of cuts and the method of Cauchy sequences are equivalent. Once you play with cuts for a while, you may understand why I came at the real numbers with Cauchy sequences first. The cut approach seems to have a certain simplicity, and it’s less ontologically demanding since we’re only ever talking about pairs of subsets of the rational numbers rather than gigantic equivalence classes of sequences. But in the end I always find cuts to be extremely difficult to work with. Luckily, once we’ve shown them to be equivalent to Cauchy sequences it will establish that the real numbers we’ve been talking about are Dedekind complete, and we can put the messiness of this definition behind us.
Like this:
Like Loading...
Related
December 5, 2007 -
Posted by John Armstrong |
Fundamentals, Numbers, Orders
The Unapologetic Mathematician 
You’ve incorrectly defined products and quotients of cuts. For example, by your definition, the right set of the square of the cut corresponding to -2 includes the product of 100 and -2, which is -200 (and the left set is empty).
Never mind, I see the qualifier “positive cut.” You may delete my comment if you wish to avoid confusing your other readers.
No, it’s worth emphasizing: the definitions of multiplication and reciprocals only apply to positive cuts. With more work you can manage to define it for all numbers, but it gets to be a huge pain, and what I’ve defined is enough to specify the field structure.
A nitpicky comment: you want to define your ordered set to be Dedekind complete if every non-empty set $S$ which possesses an upper bound possesses a least upper bound. (If $S$ is the set of reals, then every real is vacuously an upper bound of the empty set, etc.).
Ah, you’re right, Todd. I’ll tweak that.
[…] used Dedekind cuts to “complete” the order on the rational numbers — to make sure that every […]
Pingback by Cuts and Sequences are Equivalent « The Unapologetic Mathematician | December 7, 2007 |
According to John Conway (see On Numbers And Games), constructing the reals via Dedekind cuts is enough of a pain — what with all the special cases for multiplication — that it’s worth considering taking the construction as far as the rationals in the traditional way, and then building the reals as a subset of the surreals.
Mark Chu-Carroll discussed this back in April, FWIW.
Blake, I do like the surreals, but ultimately they always feel more like a curiosity or a nonstandard model than they do a useful construction. To be honest, I wouldn’t talk about cuts at all if it weren’t just so much easier to show the Dedekind-completeness of the reals with them than with Cauchy sequences.
[…] Whether we use Dedekind cuts or Cauchy sequences to construct the ordered field of real numbers (and it doesn’t matter […]
Pingback by Archimedean Fields « The Unapologetic Mathematician | December 7, 2007 |
And what would life be like without curiosities? 😉
Still, your point is taken (I just have a tendency to note these things “for the record”).
Asking for all upper-bounded sets to have a sup seems basically the same as asking for Cauchy-completeness.
They’re similar, but distinct. Upper-bounded sets are not necessarily sequences, which are key to the idea of Cauchy completeness. Cauchy sequences, on the other hand, are not required to increase to their limit.
But this similarity does point the way towards showing that the two completions of the real numbers are equivalent. The explicit isomorphism is in the next post.
Oh, nice! Thanks for the extra details.
I was actually thinking more along the lines that you say that lack of Dedekind-completeness is a “flaw” in ℚ, which is a word common in mathematical rhetoric that I’ve never understood. (Ditto for “nice”.) I get why ℚ doesn’t have this property, but not why that’s bad.
Well, it depends what you want to do with it. For pure algebra, that’s fine. When you want to take limits, though, things become a problem. Let’s say, for instance, you want to use Newton’s method — just using the iterating function, not bothering with where it comes from — to solve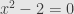
. You set up a sequence with 
and
This is a purely algebraic function, and every time we start with a rational input we’ll get a rational output. That is,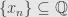
. You can even show that it’s Cauchy. But what’s the limit of the sequence? If you only have the rational numbers to work with, this is a sequence that cannot converge even though we have a really simple, practical reason to want it to.