Presheaves
Strictly speaking, sheaves are not just about differential topology. And it’s also possible to get away without talking about them explicitly in differential topology. But it’s in differential topology that they really start to make their presence felt.
The best description of a sheaf I ever got doesn’t really translate to text, unfortunately. I forget the originator, as told to me by the professor explaining it — and if he remembers and can fill in the gap this can be recorded for posterity — but it really does capture the essence. A sheaf is a thing where the topology goes this way (moving one’s open hand around in circles at about chest level) and the algebra goes this way (moving one’s hand up and down across chest level). To be a bit more explicit, sheaves are about taking algebraic structures and localizing them to open sets in a topological space. I’ll start with the simplest versions, which are sheaves of sets. Further, I’ll actually start with something simpler: presheaves.
So, a presheaf of sets on a topological space
is a choice of a set
for each open set
. We call the members of
the elements — or the “sections” — of the presheaf “over
“. But there’s an important condition on this choice: if
is a smaller open subset of
, then we should be able to “restrict” our element
to an element
. Thus, if we have an inclusion
, then we have a restriction map
.
These restriction maps are subject to a couple conditions. First of all, if we restrict from to itself, then we shouldn’t change anything. That is, the restriction map
is always the identity map. Secondly, if we restrict from
to
, and then from
to
, we should get the same result as if we just restricted directly from
to
. That is, we have the equation
. Because of this, we’ll often just write the restriction map as
, since which subset it came from doesn’t really matter.
We can express this definition more succinctly if we remember that containment of open subsets of a topological space constitutes a partial order, and thus defines a category . The objects are the open sets themselves, and there is a unique arrow from
to
if
. If we look closely, we’ll find that what we’ve defined as a presheaf is actually a contravariant functor from this category to the category of sets! For every arrow
we have an arrow
— in the “opposite direction”, since the functor is contravariant. The conditions we impose on the restriction maps just say that they preserve identity arrows and compositions.
Now, there’s nothing inherently special about sets here. We can set up exactly the same construction with any target category to define, say, a presheaf of rings to be a contravariant functor . This assigns a ring
to every open set
, and the restriction maps have to be ring homomorphisms. In the same way we get presheaves of groups, of abelian groups, or of vector spaces over a given field.
The one possibly confusing case is when we talk about a presheaf of modules over a presheaf of rings. In this case, say we have a presheaf of rings on a topological space
. A presheaf of modules
over
assigns an abelian group
to every open set
— it’s a presheaf of abelian groups — in such a way that
is a module over
. The restriction map has to work with the restriction map of
, so we have
.
The canonical example to keep in mind is continuous, real-valued functions on a topological space. This is a sheaf of real algebras that associates to the open set the algebra
of real-valued functions that are defined and continuous there. Clearly we can restrict such a function
to whatever open subset
we want — and, in fact, we have. The nice thing is that this gives us a way of talking about and dealing with functions on our space that may not be defined or continuous everywhere. Just work within a suitable open set where the function does play nice! If you need to work with two functions defined over different open sets, just restrict them both to their common intersection and work there. Many structures we run into in differential geometry will be naturally expressible in terms of presheaves, just like this.

I’m having a bit of trouble figuring out what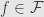 is in paragraph 3. A member of the set that is the value of the presheaf at
is in paragraph 3. A member of the set that is the value of the presheaf at 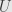 ? Or something different?
? Or something different?
I mean .
.
Exactly. If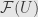 is a set, then
is a set, then  is an element of that set. I chose
is an element of that set. I chose 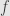 because of the example listed in the last paragraph. Maybe it would help to read that example and then go back through the definition to see how it fits.
because of the example listed in the last paragraph. Maybe it would help to read that example and then go back through the definition to see how it fits.
[…] the moment we will be more concerned with presheaves, but we may as well go ahead and define sheaves. These embody the way that not only can we restrict […]
Pingback by Sheaves « The Unapologetic Mathematician | March 17, 2011 |
Got it. I wouldn’t have had a problem if “these are” was replaced by “the members of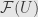 are”.
are”.
In the 4th paragraph, I do not understand why the equation is not written the other way around, with restriction from U to V written on the right of restriction from V to W
You’re right, it probably should be written the other way. Thanks.
John, I heard the “this way – that way” description of sheaves from Bill Massey. You might have been there at the time, or you might have gotten it from me later, since I certainly worked that description into my repertoire. I still use it whenever I talk about sheaves to a broad audience.
By the way, in the penultimate paragraph, it might be less confusing to write $(fm)|_V=f|_V m|_V$, both because on the left hand side you’re restricting all of $fm$ and also because $f(m)$ looks like you’re evaluating some function at $m$.
In the last paragraph, shouldn’t it be ‘presheaf’ not ‘sheaf’ (a sheaf seems to need an extra restriction).
Avery, it turns out that the continuous real-valued functions do form a sheaf. But since a sheaf is a presheaf, it’s an example of the latter as well.
[…] Between Presheaves As ever, we want our objects of study to be objects in some category, and presheaves (and sheaves) are no exception. But, luckily, this much is […]
Pingback by Mappings Between Presheaves « The Unapologetic Mathematician | March 19, 2011 |
Regarding the bit about doing topology horizontally and algebra vertically: somewhere I read a riff on this as follows. ‘Sheaf’ in ordinary English can mean something like a bundle of stalks, the stalks being aligned vertically. Or, it can mean a sheaf of papers, each leaf lying horizontally (like a section of a sheaf). The word play is supposed to be even better with the French equivalent faisceau.
I wish I could remember where I read this; I’m pretty sure it was in some categorical discussion about sheaves.
[…] Direct Image Functor So far our morphisms only let us compare presheaves and sheaves on a single topological space . In fact, we have a category of sheaves (of sets, by […]
Pingback by The Direct Image Functor « The Unapologetic Mathematician | March 21, 2011 |
[…] more construction we’ll be interested in is finding the “stalk” of a presheaf over a point . We want to talk about how a presheaf behaves at a single point, but a single point […]
Pingback by The Stalks of a Presheaf « The Unapologetic Mathematician | March 22, 2011 |
[…] of Functions on Manifolds Now that we’ve talked a bunch about presheaves and sheaves in general, let’s talk about some particular sheaves of use in differential […]
Pingback by Sheaves of Functions on Manifolds « The Unapologetic Mathematician | March 23, 2011 |
[…] subspace we can restrict a vector field on to one on , which means we’re talking about a presheaf. In fact, it’s not hard to see that we can uniquely glue together vector fields which agree […]
Pingback by Vector Fields « The Unapologetic Mathematician | May 23, 2011 |
Iterated integration of multi-integrals seems to constitute a presheaf where the topological space is $\{ 1, …, n \}$ and $F(U)$ is the set of integrable functions $f(x_k | k \in U)$ (e.g. $f(x_2, x_3, x_5)$ for $U = \{ 2, 3, 5 \}$). The restriction map $U \rightarrow V$ is integration over $(x_k | k \in U \ V)$.