The Existence Theorem for Limits
Of course, though we’ve defined limits, we don’t know in general whether or not they exist. Specific limits in specific categories have been handled in an ad hoc manner. We show that the Cartesian product is a product in , or that there is a subset which equalizes a pair of morphisms, but we have been doing this all by hand and there are so many different kinds of limits that it’s impossible to handle them all like this. Luckily, we can build complicated limits out of simpler ones in many cases.
In fact, we’ve already seen this: we built pullbacks from products and equalizers. Actually we explicitly built pushouts from coproducts and coequalizers, but the pullback construction is just the dual. Anyhow, that construction shows the general idea. If a category has finite products and equalizers of pairs then it has limits for all functors from finite categories
. If it has all products (indexed by arbitrary sets) as well as pairwise equalizers then it is complete. Conversely, since products and equalizers are examples of limits completeness of a category implies their existence. That is, once we have these kinds of limits all the others come for free.
The proof is summed up in this somewhat arcane diagram.
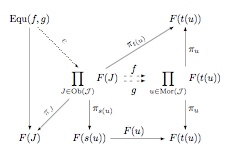
So let’s unpack it. We’re in a category and are considering a functor
, where
is either a small or a finite category.
Starting in the middle row we’ve got the product of all the objects in the image of and the product over all the morphisms of
of the images of their target objects. Now towards the top we have a projection
from the second product onto each factor, and since each factor is in the image of
we also have morphisms from the first product. There’s actually a triangle at the top for each morphism
in the category
, but we only draw one. Now by the universal property of the second product there exists a unique arrow
from the first product to the second that makes all these triangles commute.
We do a similar thing on the bottom. We again have the projections from the second product to its factors. For each morphism in there’s a projection from the first product onto the image of its source, and then there’s an arrow
from the image of the source to the image of the target. Again, there’s one such square at the bottom for each morphism in
, but we only draw one. Again, by the universal property of the second product there exists a unique arrow
from the first product to the second that makes all of these squares commute.
So now we have two parallel arrows from the first product to the second, and we take their equalizer, which gives an arrow into the first product. We also have an arrow out of the product for each object of , so we can compose to get an arrow
for each object
. I claim that this is the limit we seek.
First we need to check that this is a cone on . For an arrow
in
we need to see that
. The lower commuting square for
tells us that
. The upper commuting square tells us that
. So we calculate
as desired.
Now if is any other cone on
then the arrows in the cone combine to give a unique arrow
. Since this is a cone, we can check that
. Thus
factors uniquely through
, giving the universal property we need.
In the finite case, our discussion of multiple products shows that all we need are binary products, a terminal object, and binary equalizers to have all finite products and binary equalizers, and thus to have all finite limits. In general, infinite products have to be dealt with on their own.
Many of our algebraic categories can now be shown to be complete. For examples, each of ,
,
,
, and
is complete.
Dually, a category is cocomplete if and only if it has all coproducts and pairwise coequalizers. It has all finite colimits if and only if it has all finite coproducts and pairwise coequalizers. You should determine which of the above list of categories are cocomplete.

[…] of limits We know that the category has equalizers and all (small) products, so by the existence theorem we know it is complete. However, it will be useful to have an explicit calculation of all small […]
Pingback by Limits of sets and Creation of limits « The Unapologetic Mathematician | June 21, 2007 |
[…] and coproducts, while kernels of morphisms tell us about all different equalizers. And then The Existence Theorem for Limits tells us that every finite limit can be constructed from finite products and equalizers, while […]
Pingback by Properties of Ab-Categories « The Unapologetic Mathematician | September 17, 2007 |
Should the arrow from the first product to F(J) in the lower left of the diagram be lablled ?
?
You might think so, but notice that the product is indexed by , and so the projection morphisms are also indexed by the same
, and so the projection morphisms are also indexed by the same 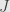 .
.
Ah, right. Another, expository, point is that this entry might be a bit easier to follow if the diagram was enlarged a bit, since, especially in printouts, the subscripts can be pretty difficult to read, especially the ones typeset slanted.
what are the proofs of some of the trigonometric limits theorems
ronaldo, you obviously have no clue what sorts of limits I’m talking about here. I’m not going to do your homework for you.
[…] now, the existence theorem for limits tells us that all limits and colimits exist in . That is, the category of topological spaces is […]
Pingback by Limits of Topological Spaces « The Unapologetic Mathematician | April 28, 2010 |
[…] attatched. It turns out that if we unpack all the category theory — basically using the existence theorem — it’s not really that […]
Pingback by The Stalks of a Presheaf « The Unapologetic Mathematician | March 23, 2011 |
Where the upper commuting square is, of course, a triangle.
Great entry!
Could I ask you for some clarifications about the very last passage?
How do you check than $fh = gh$? I understand that then we get another cone of the same type of the equalizer of $f$ and $g$, and thus we find the factorization we needed, but to do that we still have to guarantee that commutativity condition.
I thought about decomposing $h$ in the $\lambda_J$s that generates it and checking the composition “component-wise”, but I don’t know how to do this check. I suspect that the equation $\lambda_J = F(u) \circ \lambda_K$ might be involved although I didn’t manage to plug it in the correct way to get the result.
It’s been a while since I’ve thought directly about this (wow, like about ten years… I’m so old), so it’s not at the tip of my fingers. But I’ll try to dust off the cobwebs give it a go…
I think you’re actually running right up onto the deep meaning of the existence theorem, even if you don’t quite realize it yet. The whole idea is that being a cone is actually equivalent to equalizing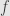 and
and 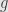 . That is, these two arrows encode two different operations, and the point of a cone is that the two are equal.
. That is, these two arrows encode two different operations, and the point of a cone is that the two are equal.
Remember that a cone consists of an object and a family of arrows
and a family of arrows  , one for each object
, one for each object  . But not any such collection works; there’s a naturality condition! For
. But not any such collection works; there’s a naturality condition! For 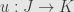 we have
we have  .
.
So, the real trick of the existence theorem (which maybe I could have explained better before), is that if you’ve got products and equalizers, you can encode this naturality condition in terms of the equalizer of two arrows in ! A cone, then, is exactly a collection of arrows
! A cone, then, is exactly a collection of arrows  such that the unique arrow into the product
such that the unique arrow into the product 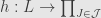 equalizes the two arrows
equalizes the two arrows 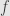 and
and 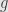 . And a limit — a universal cone — is just the equalizer of the two arrows.
. And a limit — a universal cone — is just the equalizer of the two arrows.
The key, then, is to understand how the arrows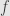 and
and 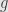 encode the naturality condition. I’ve actually done this once above, in the particular case of the equalizer, when I checked that it was a cone itself. What’s left is just to run that same argument backwards, showing that any cone equalizes the two arrows.
encode the naturality condition. I’ve actually done this once above, in the particular case of the equalizer, when I checked that it was a cone itself. What’s left is just to run that same argument backwards, showing that any cone equalizes the two arrows.
So, re-draw the left-hand triangle of the diagram, but instead of , use
, use 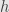 . The vertical arrow is
. The vertical arrow is 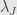 , and it should be clear why
, and it should be clear why  . Being a cone tells us that for every
. Being a cone tells us that for every 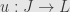
which we rewrite as
Exactly as before, we can see that and that
and that  . So again we rewrite:
. So again we rewrite:
Now, since that’s true for all , the product property (over the morphisms of
, the product property (over the morphisms of 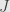 ) tells us that
) tells us that
Just as we wanted!
Thank you very much, now it’s very clear! I thought I had used all my brain resources to get to the end of the proof and then nothing remained to parse the last bit, because now it seemed very obvious.
By the way, I really appreciated the additional remark about the intuition behind the theorem. It shows the cleverness of the theorem, which is indeed quite beautiful actually.