Linking Integrals
There’s a new paper out on the arXiv discussing higher-dimensional linking integrals, by two graduate students at the University of Pennsylvania. I don’t have time to really go through it right now, but at a first scan I’m really not sure what they’ve done here. It seems they’re just taking the regular Gauss integral and doing the exact same thing for higher-dimensional spheres, although in a way that’s so loaded down with notation that it obscures the fact that it’s the exact same idea.
Some people like results that are more computationally focused, and some (like me) prefer to lay bare the structure of the concepts, and derive a computational framework later. It may be that these authors are just more the former than the latter. Anyhow, I’m not certain how original it is, but my own work is shot through with “wait, you mean nobody’s written that up yet?” If they’ve found one of these obvious niches that nobody has gotten around to mining, more power to them.

Your assessment is basically right. At least, I’ve heard people talk about these results and that’s basically the way they seem to summarize them — I don’t have time to go through the paper now either.
Ultimately my conceptual view may be in the paper, but it certainly doesn’t seem to have been emphasized at a first glance. Of course, the authors are free to present as they please, but I would find it more illuminating if the paper centered on the idea of a map from to
to 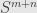 , and then calculating the (signed) number of times that this map covers the target sphere. Then the calculations can follow afterwards as a way of getting at this topological intuition.
, and then calculating the (signed) number of times that this map covers the target sphere. Then the calculations can follow afterwards as a way of getting at this topological intuition.
Since the arXiv isn’t a weblog, maybe a graduate student in their department could point them at this thread (hint, hint)?
I haven’t read this preprint properly so this may be way off base, but…
There is an existing theory, isn’t there? Tadayuki Watanabe has a research programme involving higher dimensional claspers which is actually quite developed- he can recover K-theoretical calculations of characteristic classes of unknots from his formulae, and the connection with configuration space integrals is quite explicit.
References:
On Kontsevich’s characteristic classes for smooth 5- and 7-dimensional homology sphere bundles math/0610292
Configuration space integral for long n-knots, the Alexander polynomial and knot space cohomology math/0609742
Clasper-moves among ribbon 2-knots characterizing their finite type invariants Journal of Knot Theory and Its Ramifications, 2006; 15 (9) 1163-1200
Moreover, he is building on work of Habiro and Shima.
The other people working on this are Cattaneo and Rossi (Wilson surfaces and higher dimensional knot invariants, Comm. Math. Phys. 256 (2005) 513-537)
Cattaneo, Cotta-Ramasino, Longoni (Configuration spaces and Vassiliev classes in any dimension) Alg. Geom. Topol. 2 (2002) no.39 949-1000
Configuration space integrals (including self-linking integrals as the simplest example) were first studied I think by R. Bott, who found a CFI invariant for 2-knots (I can’t now find the reference, but it should easily be traceable).
Please refer them to the above papers. I think T. Watanabe’s work certainly should at least be cited, even if these students are doing something substantially new (which I can’t at the moment see).
John Armstrong-
Of course, the authors are free to present as they please, but I would find it more illuminating if the paper centered on the idea of a map from to , and then calculating the (signed) number of times that this map covers the target sphere. Then the calculations can follow afterwards as a way of getting at this topological intuition.
This is the view of the Watanabe papers I believe.
Watanabe’s work is actually quite impressive and far reaching I think- he can calculate all kinds of cool stuff, in quite a general setting.
Correction to typo in post 3:
characteristic classes of homology sphere bundles.
Daniel, thanks for the references. I’m sure if the authors visit here they’ll find them very helpful. As for myself, it’s such a natural idea that I’m not surprised to see it’s been done before. In this light, I’d advise the authors of the new paper to scour these references and determine how, if at all, their computational method differs from those that have gone before.
I’ve had to do this myself, for example… well, I’ll get back to that point in the very near future.
I admit to being a little confused by this critique because I don’t quite know what you mean by “It seems they’re just taking the regular Gauss integral and doing the exact same thing for higher-dimensional spheres”. My guess that you think we’re giving an integral which computes the linking number of two spheres in Euclidean space. This would also jibe with comment #2. Of course (as wasn’t quite stated explicitly but clearly implied), a paper whose entire content was an extension of the familiar degree-of-map argument for the Gauss integral to higher dimensional Euclidean spaces would be completely spurious. This *is* the content of our section 2, not because we are deluded enough to think it’s new (after all, it’s probably been a folk theorem for at least 50 years), but rather to give the reader a sense of our notation. We did skimp a bit on explaining the conceptual underpinnings of this argument, not because we’re particularly enamored with elaborate computations, but rather because we believed that anybody reading this paper would already be familiar with the conceptual underpinnings of the degree-of-map proof of the Gauss integral.
The reason we included section 2 was because we wanted to use the Gauss linking integral in, say, R^{n+1} to derive an integral which will compute the linking number of two submanifolds of, say, S^n. We can’t directly apply the Gauss integral in R^{n+1} because the codimensions are wrong. For example, two Hopf circles are linked when viewed as submanifolds of S^3, but can easily be pulled apart in R^4. Instead, we need to convert one of the submanifolds of S^n to a (singular) submanifold of R^{n+1} of one higher dimension (so that the codimensions are right) and then use the linking integral in R^{n+1}. We do this in such a way that, first, the linking number of the new pair is the same as that of the old pair and, second, we can integrate out the extra dimension so that we get something intrinsic to S^n.
Incidentally, we can’t just copy the degree-of-map proof for spheres. The derivation of the Gauss linking integral in R^3 (resp. R^n), relies crucially on the fact that the configuration space of two distinct points in R^3 deformation retracts to S^2 (resp. S^{n-1}). This is precisely the the target sphere when defining the “degree” map S^1 x S^1 -> S^2 (resp. K x L -> S^{n-1}). There’s a technical problem, however, when we try to apply this argument to spheres. Since [using n=3 as the simplest example] the configuration space of 2 distinct points on S^3 deformation retracts to the antipodal S^3, any map from S^1 \times S^1 to the configuration space will be homotopically trivial. In other words, there is no hope of generalizing the degree-of-map derivation of the linking integral to spheres, much less any other manifold.
Though this approach is new, our linking integral in S^n is not completely new, either: an equivalent integral formula for the linking number of two closed submanifolds of S^n is proved in a forthcoming paper of DeTurck and Gluck and also can be generalized from an argument in Greg Kuperberg’s “From the Mahler conjecture to Gauss linking forms” (math/0610904).
What is new is that our technique works just as well in giving integral formulas for the linking number of closed, null-homologous submanifolds of S^n \times R^m or any other “visible hypersurface” (which we define as a hypersurface such that any ray from the origin intersects it not at all or exactly once, where the single intersection, if it exists, should be transverse). Though S^n and S^n \times R^m are the most obvious examples, the fact that any closed manifold is homotopy equivalent to a visible hypersurface means this is a pretty general class of manifolds.
Now, you might ask yourself: why spend all that effort doing something which is topologically trivial? After all, if you want a linking integral for submanifolds of S^n, you can always just pick a point which misses both submanifolds, stereographically project to R^n and use the Gauss linking integral there.
Doing so will, of course, compute the linking number correctly, so topologically there’s no point in doing something more difficult. However, one of the very useful features of the Gauss integral is the following: not only is the integral itself invariant under link-homotopy (as, of course, it must be, since the linking number is), its integrand is invariant under orientation-preserving isometries of Euclidean space. The Gauss integral is, therefore, not just a topological gadget, but also a geometric gadget. This is handy for a number of applications.
Thus, our original motivation: find a linking integral on S^n which is geometric in the same sense as Gauss’s integral, namely that its integrand is invariant under orientation-preserving isometries of S^n. This was done in S^3 (and also in hyperbolic 3-space) by DeTurck and Gluck (math/0510388v1) along the lines of the electrodynamics proof of the Gauss integral.
Of course, there’s no hope of an electrodynamics approach working in higher dimensions, but the integral in our Corollary 1.3 is exactly such an integral. In the more general case of S^n \times R^m, the integrand in our Theorem 1.1 is, unfortunately, not completely isometry invariant: the integrand is invariant under rotation in either factor, but is not invariant under translations in the R^m factor. In the case of an arbitrary visible hypersurface, there’s even less isometry invariance, but our integral is still somewhat geometric (as indicated in the abstract and in Remark 1.2) since the integrand is invariant under the action of SO(n+1) on the hypersurface.
Sorry for going on at such excruciating length. Reading through the post and comments here was a little dispiriting, not because I think we did anything wrong mathematically, but, given the apparent misunderstandings of what we did, because it seems like we obviously didn’t do as good a job as we thought at explaining our results. If you have any suggestions for how we could improve the exposition, especially any that would have prevented such misunderstandings, I would love to hear them.
Thanks for the explanation. As I’ve said, I didn’t have the time yesterday to really go over the paper in detail, so it might be clearer on a second pass.
One thing I’ve found working recently is to write out the meaty proofs and calculations, and then go back to write an introduction that lays out exactly what I’m about to say (easier since I’ve just written it down already) and why I’m saying it. This I do informally with as little calculation and notation as possible. Of course, given my history I might not be the best person to ask about how to write a paper…
I’d like to second Clay’s remarks. And you, Clay, shouldn’t feel so discouraged, certainly not at any personal level. People in general only skim many of the papers that they see. Arguably this is dispiriting in general, but in your case it doesn’t mean that you wrote the paper badly or otherwise that there is anything wrong. In fact one of my first papers was rejected because the referee didn’t “get it”. This was no real injury to me, because when I testily explained what I had done that was new, the referee simply accepted that I was right and he was wrong.
To get back to the math, it is a very interesting fact that the integrand of the Gauss linking formula doesn’t have to be a closed differential form. The form is a function of two points on the manifold, omega(x,y), and the main necessary condition is that it be “weakly closed”, or d_x d_y omega(x,y) = 0. This condition is analogous to the pluriharmonic equation in Dolbeault cohomology. It is not quite a sufficient condition, but it is close. Moreover, as Clay explains, with extra conditions such as global topology or required symmetry, there may not even be a closed form available.
With the emphasis on symmetry, it would interesting to explore the geometric linking form for a closed hyperbolic homology sphere. There is one that comes from the the hyperbolic-invariant linking form in the universal cover of said homology sphere, and I would suppose that you can push it down to the quotient manifold.
Now I feel like I should offer a defense. I wanted to comment as quickly as possible to bring this paper some wider attention, since it seemed an interesting idea at first glance, but life being what it is I hadn’t (and still haven’t) gotten around to reading it in depth. And so I posted a clear disclaimer that I haven’t read it thoroughly and that I would get around to it when I have the time.
Greg, if I were writing a referee’s report here, I assure you that I would put much more care into the reading. But the fact is I’m not writing a referee’s report to determine publication. I’m writing a weblog post to improve publicization.
Messrs Shonkwiler and Vela-Vick shouldn’t be discouraged by my post not because “people in general only skim many of the papers that they see”, but because I fully intend to do the thorough reading the paper deserves. All in all, if I should extend an apology for giving instant publicity (however minor), then I heartily do so.
Clay,
Now That I’ve had a closer look at your paper and read your comments I see what you’re saying… and what I said initially was off-base I think- I’m sorry. Don’t be discouraged- the comment was based on a skim, and a deeper read (and definitely your comment) reveals what you said.
I’m hardly one to talk on this either, because I’ve had papers people “didn’t get” at all, but… maybe it might be a good idea to say what you said above in the introduction in a future version? What you said here I understood and made sense, and gave the context which I was missing.
Another good reason not to be discouraged- any publicity is good publicity. I know that I for one read you paper which I would not otherwise have noticed, and I’ll forward it to other people who might be interested.
The other difference I wasn’t noticing is that the references I gave concern one submanifold, where there are configuration space integral topological invariants, whereas the case of the linking of two submanifolds is manifestly different.
With the emphasis on symmetry, it would interesting to explore the geometric linking form for a closed hyperbolic homology sphere. There is one that comes from the the hyperbolic-invariant linking form in the universal cover of said homology sphere, and I would suppose that you can push it down to the quotient manifold.
Hmm…that is an interesting question. As you say, it seems like the invariant form ought to descend to the quotient, but I’d need to think about it more.
By the way, thank you John, Daniel and Greg for taking the time to think about and discuss our paper. Obviously we hoped someone would take notice when we posted it, but it’s certainly gratifying to see people whose work I’ve read and enjoyed talking about it less than 24 hours after it went public.
Now I feel like I should offer a defense.
It’s all cool as far as I’m concerned. Yes, blog discussions are more informal than, say, published papers. Been there, done that — I was one of the moderators of sci.math.research for a number of years and I posted there many times.
Anyway, mainly I meant to explain some of the mathematical context.