Change of Variables in Multiple Integrals II
Okay, let’s get to actually proving the change of variables formula for multiple integrals. To be explicit:
Let be a continuously differentiable function defined on an open region
. Further, assume that
is injective and that the Jacobian determinant
is everywhere nonzero on
. The inverse function theorem tells us that we can define a continuously differentiable inverse
on all of the image
.
Further, let be a Jordan measurable subset of
, and let
be defined and continuous on
. Then we have the change of variables formula
We will proceed by induction on the dimension . For
, this is exactly the one-dimensional change of variables formula, which we already know to be true. And so we’ll assume that it holds in all
-dimensional cases, and prove that it then holds for
-dimensional cases as well.
Since the Jacobian determinant is nonzero, we cannot have
for all
; at least one of the components must have a nonzero partial derivative with respect to
at any given point
. Let’s say, to be definite, that
. We will now (locally) factor
into the composite of two functions
and
, which will each have their own useful properties. First, we will define
This is clearly continuously differentiable, and it’s even injective on some neighborhood of , by our assumption that
. Further, the Jacobian determinant
is exactly the partial derivative
, and so the inverse function theorem tells us that in some neighborhood of
we have a local inverse
, with
in some neighborhood of
. We can now define
for , and define
Then for each in a small enough neighborhood of
we have
. The first function
leaves all components of
fixed except for
, while the second function
leaves
fixed. Of course, if we used a different partial derivative
, we could do the same thing, replacing
instead with
in
, and so on.
Now if is a Jordan measurable compact subset of
, then its inverse image
will also be compact since
is continuous. For every point in
, we can find some neighborhood — which we can take to be an
-dimensional interval — and a factorization of
into two functions as above. As we move around, these neighborhoods form an open cover of
. And since
is compact, we can take an open subcover.
That is, we can cover by a finite collection of open intervals
, and within each one we can write
, where the function
leaves all the components of
fixed except for the last, while
leaves that last one fixed. By subdividing these intervals, we can assume that they’re nonoverlapping. Of course, if we subdivided into open sets we’d miss the shared boundary between two subintervals. So we’ll include that boundary in each subinterval and still have
nonoverlapping intervals
.
Then we can define . Since
is injective, these regions will also be nonoverlapping. And they’ll cover
, just as
covered
. So we can define
and write
Our proof will thus be complete if we can show that the change of variables formula holds for these regions, and we will pick up with this final step next time.

[…] far, we’ve shown that we can chop up into a collection of nonoverlapping regions and into their preimages . […]
Pingback by Change of Variables in Multiple Integrals III « The Unapologetic Mathematician | January 7, 2010 |
Don’t you mean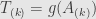 ?
?
Yes, thanks. Fixed.
“replacing instead with
instead with  in
in  , and so on.” Did you mean
, and so on.” Did you mean  ? Also, it would be nice if you could explain how to construct
? Also, it would be nice if you could explain how to construct  and
and 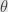 in the case when k \neq n .
in the case when k \neq n .
Thanks.
I think that’s correct; it may even be clearer to replace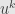 with
with  , though replacing
, though replacing  still works. Now we have
still works. Now we have  . The construction of
. The construction of 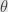 from this point should also be clearer.
from this point should also be clearer.
Thanks a lot….