Measurable Spaces, Measure Spaces, and Measurable Functions
We’ve spent a fair amount of time discussing rings and -rings of sets, and measures as functions on such collections. Now we start considering how these sorts of constructions relate to each other.
A “measurable space” is some set and a choice of a
-ring
of subsets of
. We call the members of
the “measurable sets” of the measurable space. This is not to insinuate that
is the collection of sets measurable by some outer measure
, nor even that we can define a nontrivial measure on
in the first place. Normally we just call the measurable space by the same name as the underlying set
and omit explicit mention of
.
Since it would be sort of silly to have points that can’t be discussed, we add the assumption that every point of is in some measurable set. Commonly, it’s the case that
itself is measurable —
— but we won’t actually require that
be a
-algebra.
A “measure space” is a measurable space along with a choice of a measure on the
-ring
. As before, we will usually call a measure space by the same name as the underlying set
and omit explicit mention of the
-ring and measure. Measure spaces inherit adjectives from their measures; a measure space is called finite, or
-finite, or complete if its measure
is finite,
-finite, or complete, respectively.
Given a measure space , we will routinely use without comment the associated outer measure
and inner measure
on the hereditary
-ring
.
As an underlying set equipped with a particular collection of “special” subsets, a measurable space should remind us of a topological space, and like topological spaces they form a category. Remember that our original definition of a continuous function: given topological spaces and
, a function
is continuous if the preimage of any open set is open — for any
we have
.
We define a “measurable function” similarly: given measurable spaces and
, a function
is measurable if the preimage of any measurable set is measurable — for any
we have
. It’s straightforward to verify that the collection of measurable spaces and measurable functions forms a category. We will set this category in its full generality aside for the moment, as is the usual practice in measure theory, but we will refer to it if appropriate to illuminate a point.
Before I close, though, I’d like to put out a question that I don’t know the answer to, and which some friends haven’t really been able to answer when I mused about it in front of them. When we dealt with topology, we were able to recast the basic foundations in terms of nets. That is, a function is continuous if and only if it “preserves limits of convergent nets” — if it sends any convergent net in the domain to another convergent net in the range, and the action of the function commutes with passage to the limit. I like this because the idea of “preserving” some structure (albeit an infinite and often-messy one) feels more natural and algebraic that the idea of inspecting preimages of open sets. And so I put the question out to the audience: what is “preserved” by a measurable function, in the same way that continuous functions preserve limits of convergent nets?

is it enough [tex] mathcal{S} [/tex] be a [tex] \sigma ring [/tex] a probability book i’m studying says the space needs a [tex] \sigma – Field[/tex]
Could you clarify please
thanks
A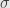 -field is a different name for a
-field is a different name for a 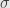 -algebra. As I point out above, in many cases
-algebra. As I point out above, in many cases  actually is a
actually is a 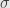 -algebra (or -field). In this case,
-algebra (or -field). In this case, 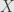 itself is in
itself is in  , and so it’s clear that every point in
, and so it’s clear that every point in 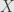 is in some measurable set.
is in some measurable set.
However, we’re going to allow to just be a
to just be a 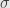 -ring —
-ring — 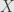 itself might not be in
itself might not be in  — so long as every point in
— so long as every point in 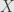 is still in some measurable set.
is still in some measurable set.
[…] we’re considering the category of measurable spaces it’s a natural question to ask whether a subset of a measurable space is itself a […]
Pingback by Measurable Subspaces I « The Unapologetic Mathematician | April 28, 2010 |
[…] Subspaces III To recap: we’ve got a measure space and we’re talking about what structure we get on a subset . If is measurable — if […]
Pingback by Measurable Subspaces III « The Unapologetic Mathematician | April 29, 2010 |
[…] more general version of integration. When we couple this with our slightly weakened definition of a measurable space, this necessitates a slight tweak to our definition of a measurable […]
Pingback by Measurable (Extended) Real-Valued Functions « The Unapologetic Mathematician | April 30, 2010 |
[…] we may have broken composability. We didn’t even say much about it when we defined the category of measurable spaces, because for most purposes it’s just like in topological spaces: given measurable functions […]
Pingback by Composing Real-Valued Measurable Functions I « The Unapologetic Mathematician | May 4, 2010 |
[…] two classes of functions that are very easy to work with. As usual, we’re working in some measurable space […]
Pingback by Simple and Elementary Functions « The Unapologetic Mathematician | May 11, 2010 |
[…] is a non-negative integrable function on a measure space . For every measurable set , we […]
Pingback by An Alternate Approach to Integration « The Unapologetic Mathematician | June 18, 2010 |
[…] Measurable Spaces Now we return to the category of measurable spaces and measurable functions, and we discuss product spaces. Given two spaces and , we want to define a -ring of measurable […]
Pingback by Product Measurable Spaces « The Unapologetic Mathematician | July 15, 2010 |
[…] Back and Pushing Forward Structure Remember that we defined measurable functions in terms of inverse images, like we did for topological spaces. So it should be no surprise that we […]
Pingback by Pulling Back and Pushing Forward Structure « The Unapologetic Mathematician | August 2, 2010 |
Is every measurable space is topological space
Not in any natural way. The obvious thing would be to try to use the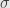 -algebra of measurable sets as the collection of open sets in the topology, but it’s not necessarily closed under arbitrary unions.
-algebra of measurable sets as the collection of open sets in the topology, but it’s not necessarily closed under arbitrary unions.
Actually my query is as follows:
If T is a sigma-algebra In X, is T also a topology in X?
No, as I said;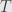 is not necessarily closed under arbitrary (uncountable) unions.
is not necessarily closed under arbitrary (uncountable) unions.