The Radon-Nikodym Chain Rule

Today we take the Radon-Nikodym derivative and prove that it satisfies an analogue of the chain rule.

If $\lambda$ , $\mu$ , and $\nu$ are totally $\sigma$ -finite signed measures so that $\nu\ll\mu$ and $\mu\ll\lambda$ , then $\lambda$ -a.e. we have

$\displaystyle\frac{d\nu}{d\lambda}=\frac{d\nu}{d\mu}\frac{d\mu}{d\lambda}$

By the linearity we showed last time, if this holds for the upper and lower variations of $\nu$ then it holds for $\nu$ itself, and so we may assume that $\nu$ is also a measure. We can further simplify by using Hahn decompositions with respect to both $\lambda$ and $\mu$ , passing to subspaces on which each of our signed measures has a constant sign. We will from here on assume that $\lambda$ and $\mu$ are (positive) measures, and the case where one (or the other, or both) has a constant negative sign has a similar proof.

Let’s also simplify things by writing

$\displaystyle\begin{aligned}f&=\frac{d\nu}{d\mu}\\g&=\frac{d\mu}{d\lambda}\end{aligned}$

Since $\mu$ and $\nu$ are both non-negative there is also no loss of generality in assuming that $f$ and $g$ are everywhere non-negative.

So, let $\{f_n\}$ be an increasing sequence of non-negative simple functions converging pointwise to $f$ . Then monotone convergence tells us that

$\displaystyle\begin{aligned}\lim\limits_{n\to\infty}\int\limits_Ef_n\,d\mu&=\int\limits_Ef\,d\mu\\\lim\limits_{n\to\infty}\int\limits_Ef_ng\,d\lambda&=\int\limits_Efg\,d\lambda\end{aligned}$

for every measurable $E$ . For every measurable set $F$ we find that

$\displaystyle\int\limits_E\chi_F\,d\mu=\mu(E\cap F)=\int\limits_{E\cap F}\,d\mu=\int\limits_{E\cap F}g\,d\lambda=\int\limits_E\chi_Fg\,d\lambda$

and so for all the simple $f_n$ we conclude that

$\displaystyle\int\limits_Ef_n\,d\mu=\int\limits_Ef_ng\,d\lambda$

Passing to the limit, we find that

$\displaystyle\nu(E)=\int\limits_E\,d\nu=\int\limits_Ef\,d\mu=\int\limits_Efg\,d\lambda$

and so the product $fg$ serves as the Radon-Nikodym derivative of $\nu$ in terms of $\lambda$ , and it’s uniquely defined $\lambda$ -almost everywhere.

July 12, 2010 - Posted by John Armstrong | Analysis, Measure Theory

10 Comments »

[…] Corollaries of the Chain Rule Today we’ll look at a couple corollaries of the Radon-Nikodym chain rule. […]

Pingback by Corollaries of the Chain Rule « The Unapologetic Mathematician | July 13, 2010 | Reply
Could you quickly clarify why there is no loss of generality in assuming that f and g are everywhere non-negative? Sorry for the frequent recent posts, and thank you for the great resource too!

Comment by Bobby Brown | March 30, 2011 | Reply
Basically, if they’re not you can always decompose into positive and negative parts, use the result there, and put everything back together.

Comment by John Armstrong | March 30, 2011 | Reply
Could anyone tell me, were we exactly use the increasing sequences and why? I dont really see it 🙂

Comment by Wiebs91 | November 16, 2012 | Reply
You mean where we use the fact that the sequence $\{f_n\}$ is increasing? That’s a requirement of the monotone convergence theorem.

Comment by John Armstrong | November 16, 2012 | Reply
I know that theorem. I just wanted to know why we need it here, where it is used in the last part V(E)=… . I’m sorry, im really not used to this notations at all and don’t get the point of it by now

Comment by Wiebs91 | November 16, 2012 | Reply
Okay, well the point is that any measurable function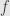 $f$ can be approximated as the limit of an increasing sequence of measurable functions 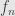$f_n$ , and the simple functions are basically constants times characteristic functions. So what we do is prove our result for the characteristic functions $\chi(F)$ . Then the fact that everything in sight is linear means that it holds for simple functions. And finally we can pass to the limit (using monotone convergence) and get the result for all measurable functions.

Comment by John Armstrong | November 16, 2012 | Reply
Ah, now I see it, thanks for your time an help 🙂

Comment by Wiebs91 | November 16, 2012 | Reply
how do we know fg is lamda-integrable?

Comment by egfdgfg | April 2, 2015 | Reply
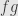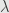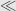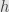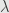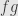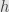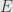Because $fg$ is the Radon-Nikodym derivative of $\nu$ with respect to $\lambda$ . To put it another way, you know that there has to be one, since $\nu\ll\lambda$ (because $\ll$ is transitive), so we can call it $h$ , and it’s uniquely defined ( $\lambda$ -a.e.). 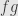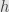But the product $fg$ satisfies the same condition as $h$ : you can get the $\nu$ -measure of any set $E$ by integrating either $fg$ or $h$ with respect to 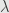$\lambda$ over $E$ . 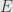So they’re equal 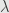$\lambda$ -a.e. and 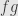$fg$ must be 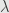$\lambda$ integrable, and so it’s as good a representative for the Radon-Nikodym derivative as any.

Comment by John Armstrong | April 2, 2015 | Reply

About this weblog

This is mainly an expository blath, with occasional high-level excursions, humorous observations, rants, and musings. The main-line exposition should be accessible to the “Generally Interested Lay Audience”, as long as you trace the links back towards the basics. Check the sidebar for specific topics (under “Categories”).

I’m in the process of tweaking some aspects of the site to make it easier to refer back to older topics, so try to make the best of it for now.

RSS Feeds

RSS - Posts
RSS - Comments
Feedback

Got something to say? Anonymous questions, comments, and suggestions at Formspring.me!
Subjects

Subjects
Archives

July 2010

M T W T F S S

1 2 3 4

5 6 7 8 9 10 11

12 13 14 15 16 17 18

19 20 21 22 23 24 25

26 27 28 29 30 31

« Jun Aug »
Search for:

The Unapologetic Mathematician

Mathematics for the interested outsider