Clairaut’s Theorem

Now for the most common sufficient condition ensuring that mixed partial derivatives commute. If $f$ is a function of $n\geq2$ variables, we can for the moment hold the values of all but two of them constant. We’ll only consider two variables at a time, which will simplify our notation. For the moment, then, we write $f(x,y)$ . We will also assume that $f$ is real-valued, and deal with vector values one component at a time.

I assert that if the partial derivatives $D_xf$ and $D_yf$ are continuous in a neighborhood of the point $(a,b)$ , and if the mixed second partial derivative $D_{y,x}f$ exists and is continuous there, then the other mixed partial derivative $D_{x,y}f$ exists at $(a,b)$ , and we have the equality

$\displaystyle\left[D_{x,y}f\right](a,b)=\left[D_{y,x}f\right](a,b)$

By definition, within the neighborhood in the statement of the theorem the partial derivative $\frac{\partial f}{\partial y}$ is given by the limit

$\displaystyle\left[D_yf\right](x,y)=\lim\limits_{k\to0}\frac{f(x,y+k)-f(x,y)}{k}$

So the numerator of the difference quotient defining the desired mixed partial derivative is

$\displaystyle\begin{aligned}\left[D_yf\right](a+h,b)-\left[D_yf\right](a,b)=&\lim\limits_{k\to0}\frac{f(a+h,b+k)-f(a+h,b)}{k}\\-&\lim\limits_{k\to0}\frac{f(a,b+k)-f(a,b)}{k}\end{aligned}$

For a fixed $k$ , we define the function

$\displaystyle g_k(t)=f(a+t,b+k)-f(a+t,b)$

We compute the derivative of $g_k$ as

$\displaystyle g_k'(t)=\left[D_xf\right](a+t,b+k)-\left[D_xf\right](a+t,b)$

so we can apply the mean value theorem to write

$\displaystyle\left[D_yf\right](a+h,b)-\left[D_yf\right](a,b)=\lim\limits_{k\to0}\frac{g_k(h)-g_k(0)}{k}=\lim\limits_{k\to0}\frac{hg_k'(\bar{h})}{k}$

for some $\bar{h}$ between ${0}$ and $h$ . We use the above expression for $g_k'$ to write the difference quotient

$\displaystyle\frac{\left[D_yf\right](a+h,b)-\left[D_yf\right](a,b)}{h}=\lim\limits_{k\to0}\frac{\left[D_xf\right](a+\bar{h},b+k)-\left[D_xf\right](a+\bar{h},b)}{k}$

In a similar trick to the one above, we can see that $\left[D_xf\right](a+\bar{h},b+s)$ is differentiable as a function of $s$ with derivative $\left[D_{y,x}f\right](a+\bar{h},b+s)$ . And so the mean value theorem tells us that we can write our difference quotient as

$\displaystyle\frac{\left[D_yf\right](a+h,b)-\left[D_yf\right](a,b)}{h}=\lim\limits_{k\to0}\left[D_{y,x}f\right](a+\bar{h},\bar{y})$

for some $\bar{y}$ between $b$ and $b+k$ .

And so we come to try taking the limit

$\displaystyle\lim\limits_{h\to0}\lim\limits_{k\to0}\left[D_{y,x}f\right](a+\bar{h},\bar{y})=\left[D_{y,x}f\right](a,b)$

If $\bar{h}$ didn’t depend in its definition on $k$ , this would be easy. First we could let $k$ go to zero, which would make $\bar{y}$ go to $b$ , and then letting $h$ go to zero would make $\bar{h}$ go to zero as well. But it’s not going to be quite so easy, and limits in two variables like this usually call for some delicacy.

Given an $\epsilon>0$ , there (by the assumption of continuity) is some $\delta>0$ so that

$\displaystyle\lvert\left[D_{y,x}f\right](x,y)-\left[D_{y,x}f\right](a,b)\rvert<\frac{\epsilon}{2}$

for $(x,y)$ within a radius $\delta$ of $(a,b)$ . As long as we keep $\lvert h\rvert$ and $\lvert k\rvert$ below $\frac{\delta}{2}$ , the point $(a+\bar{h},\bar{y})$ will be within this radius. So we can keep $h$ fixed at some small enough value, and find that $\lvert k\rvert<\frac{\delta}{2}$ implies the inequality

$\displaystyle\lvert\left[D_{y,x}f\right](a+\bar{h},\bar{y})-\left[D_{y,x}f\right](a,b)\rvert<\frac{\epsilon}{2}$

Now we can take the limit as $k$ goes to zero. As we do so, the inequality here may become an equality, but since we kept it below $\frac{\epsilon}{2}$ , we still have some wiggle room. So, if $\lvert h\rvert<\frac{\delta}{2}$ , we have the inequality

$\displaystyle\left\lvert\lim\limits_{k\to0}\left[D_{y,x}f\right](a+\bar{h},\bar{y})-\left[D_{y,x}f\right](a,b)\right\rvert\leq\frac{\epsilon}{2}<\epsilon$

which gives us the limit we need.

Of course we could instead assume that the second mixed partial derivative exists and is continuous near $(a,b)$ , and conclude that the first one exists and is equal to the second.

October 15, 2009 - Posted by John Armstrong | Analysis, Calculus

15 Comments »

[…] student. In reading this great expository blog on mathematics, I finally found a reference to a named theorem about it. And the name is not Young’s Theorem, as I have been taught. I learn something every day. […]

Pingback by Clairaut’s Theorem « Economics and Mechanisms | October 16, 2009 | Reply
Is this all you do everyday? Write dumb posts that you can get in any book? What is the usefulness of this in real life? Its not helping cure cancer…

Comment by John | October 16, 2009 | Reply
John, I think your comment deserves a thorough answer. I’m going to creat a new post to address it.

Comment by John Armstrong | October 16, 2009 | Reply
- Ok thanks. Bear in mind this is just my opinion.
  
  Comment by John | October 16, 2009 | Reply
[…] Curing Cancer After today’s post on Clairaut’s theorem, a commenter named “John” took offense. Although I’m not sure that’s his […]

Pingback by Not Curing Cancer « The Unapologetic Mathematician | October 16, 2009 | Reply
[…] though, that we have not contradicted Clairaut’s theorem here. Indeed, as long as and all the have continuous second partial derivatives, then so will . […]

Pingback by Higher Differentials and Composite Functions « The Unapologetic Mathematician | October 19, 2009 | Reply
[…] With Clairaut’s theorem comes the first common example of a smoothness assumption. It’s a good time to say just what […]

Pingback by Smoothness « The Unapologetic Mathematician | October 21, 2009 | Reply
[…] I said above, this is a bilinear form. Further, Clairaut’s theorem tells us that it’s a symmetric form. Then the spectral theorem tells us that we can find an […]

Pingback by Classifying Critical Points « The Unapologetic Mathematician | November 24, 2009 | Reply
Sorry that this is perhaps too late.

In one of the last steps, why do you claim that the inequality may become an equality?

Comment by Kiera | June 24, 2012 | Reply
That’s a good question. It’s a pretty common occurrence with limits. As an example, consider the limit of the sequence $\frac{1}{n}$ ; each term is strictly greater than zero, but the limit is zero.

As a higher level view (if you’re up for it), it’s really about topology. Strict inequalities (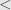 $<$ ) define open sets, while non-strict inequalities ( $\leq$ ) define closed sets. The closure of a set consists of the set itself along with all limit points, so a sequence contained in an open set (satisfying a strict inequality) may have a limit in its closure (satisfying a non-strict inequality).

Comment by John Armstrong | June 24, 2012 | Reply
- Thank you very much for such a quick response!
  
  Comment by Kiera | June 24, 2012 | Reply
In your derivation you wrote \displaystyle g_k(t)=f(a+t,b+k)-g(a+t,b) – I am wondering if it is supposed to be \displaystyle g_k(t)=f(a+t,b+k)-f(a+t,b) ? If I am mistaken I apologize.

Comment by Eric | July 23, 2014 | Reply
- Fixed, thanks.
  
  Comment by John Armstrong | July 23, 2014 | Reply
[…] only after the assumption that both mixed partials exist and are continuous. In this blog post here, the author proves a stronger […]

Pingback by Existence of mixed partials in Clairaut's theorem. - MathHub | April 3, 2016 | Reply
Thank you much for the post, I think what you do is awesome.

Comment by patrick | August 6, 2017 | Reply

About this weblog

This is mainly an expository blath, with occasional high-level excursions, humorous observations, rants, and musings. The main-line exposition should be accessible to the “Generally Interested Lay Audience”, as long as you trace the links back towards the basics. Check the sidebar for specific topics (under “Categories”).

I’m in the process of tweaking some aspects of the site to make it easier to refer back to older topics, so try to make the best of it for now.

RSS Feeds

RSS - Posts
RSS - Comments
Feedback

Got something to say? Anonymous questions, comments, and suggestions at Formspring.me!
Subjects

Subjects
Archives

October 2009

M T W T F S S

1 2 3 4

5 6 7 8 9 10 11

12 13 14 15 16 17 18

19 20 21 22 23 24 25

26 27 28 29 30 31

« Sep Nov »
Search for:

The Unapologetic Mathematician

Mathematics for the interested outsider